05. Inserting Points into KD-Tree
Header Text
Inserting Points into KD-Tree
ND312 C1 L3 A17 Inserting Points Into KD-Tree Without Quiz [LB]
Inserting Points into KD-Tree
Now let’s talk about how exactly the tree is created. At the very beginning when the tree is empty, root is NULL. The point inserted becomes the root, and splits the x region. Here is what this visually looks like, after inserting the first point (-6.2, 7).
First Point
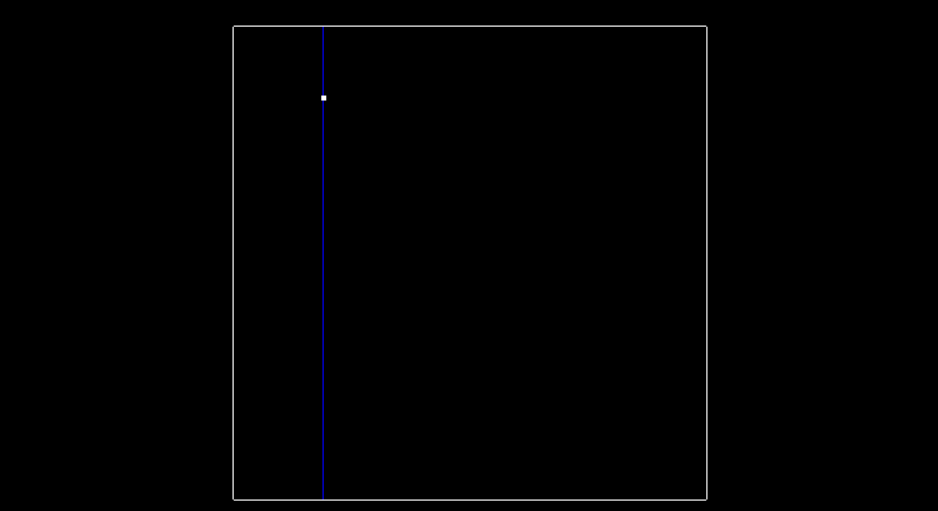
Insert first point, and split x region.
Second Point
The next point is (-6.3, 8.4). Since we previously split in the x-dimension, and -6.3 is less than -6.2. This Node will be created and be a part of root's left node. The point (-6.3, 8.4) will split the region in the y dimension.
To recap, the root was at depth 0, and split the x region. The next point became the left child of root and had a depth of 1, and split the y region.
A point at depth 2 will split the x region again, so the split dimension number can actually be calculated as depth % 2, where 2 is the number of dimensions we are working with. The image below shows how the tree looks after inserting the second point.
Second Point
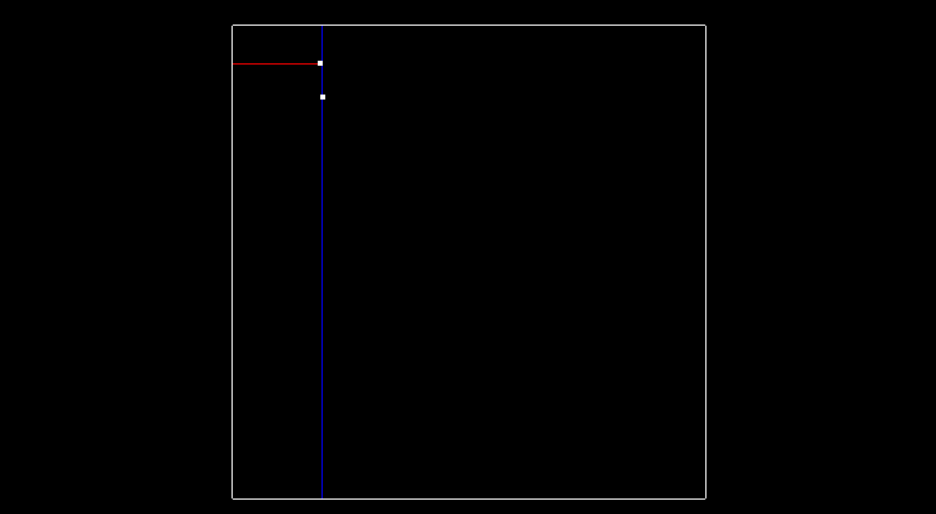
Inserting second point, splitting y region this time.
Two More Points
Then here is what the tree looks like after inserting two more points (-5.2, 7.1) and (-5.7, 6.3), and having another x split division from point (-5.7, 6.3). The tree is now at depth 2.
Two More Points
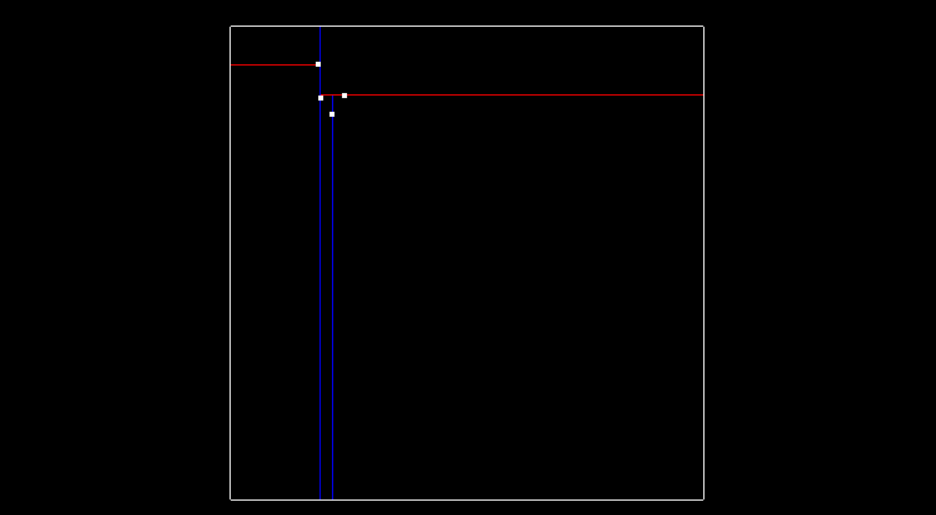
Inserting two more points, splitting x region again.
Tree Structure
The image below shows so far what the tree looks like after inserting those 4 points. The labeled nodes A, B, C, D, and E are all NULL but if the next point (7.2, 6.1) is inserted, which of those 5 nodes will the new point node be assigned to? Remember to traverse the tree starting at the root. The depth tells you which dimension (x or y) you should use for comparison.
Tree Structure
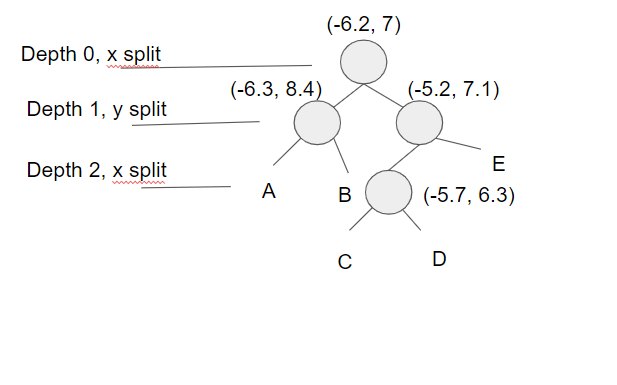
Tree structure from first four points.
Placing New Point
SOLUTION:
DSolution
ND312 C1 L3 A18 Inserting Points Into KD-Tree Solution [LB]
Improving the Tree
ND312 C1 L3 A28 Improving The Tree [LB]
Improving the Tree
Having a balanced tree that evenly splits regions improves the search time for finding points later. To improve the tree, insert points that alternate between splitting the x region and the y region evenly. To do this pick the median of sorted x and y points. For instance if you are inserting the first four points that we used above (-6.3, 8.4), (-6.2, 7), (-5.2, 7.1), (-5.7, 6.3) we would first insert (-5.2,7.1) since it is the median along the x axis. If there is an even number of elements the lower median is chosen. The next point to be inserted would be (-6.2, 7), the median of the three points for y. This would be followed by (-5.7,6.3) the lower median between the two for x, and then finally (-6.3,8.4). This ordering will allow the tree to more evenly split the region space and improve search time later.